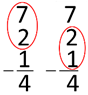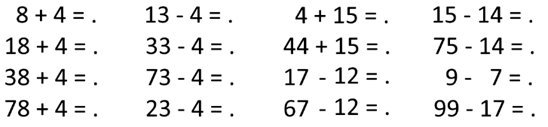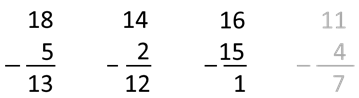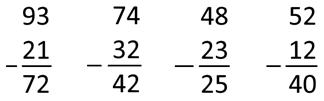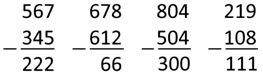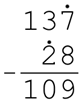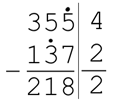|
https://www.cielen.eu/cijferen-aftrekken.htm Snel naar: Aftrekken als hoofdrekenen
(met twee termen) Aftrekken
hoofdrekenen met drie termen Werken volgens analogie (vanaf
de eerste klas) Aftrekken met een
andere schrijfwijze (tweede klas) Cijferend aftrekken (vanaf de
derde klas) Aftrekken met omruilen (vanaf de
derde klas) Controle van de gemaakte
aftrekking (alle klassen) ict:
aftrekkingen programmeren in Python (vijfde en zesde klas) Terug naar: Homepagina
(cielen.eu) De overgang van hoofdrekenen naar cijferen In de eerste en de tweede klas: uitsluitend hoofdrekenen.
Vanaf de derde klas ook cijferend aftrekken. In de eerste klas ga je tot het getal 20 met
mondelinge en schriftelijke oefeningen. Taal is hierbij zeer belangrijk,
vooral bij de mondelinge oefeningen waarbij de kinderen materialen gebruiken
zoals je dat kunt doen bij de dagelijkse mondelinge herhaling in de opmaat.
Enkele voorbeelden: 4 3 = . of
. = 4 3 Hoe
zet je deze bewerking om in taal? 1.
Je hebt 4 euro (of potloden, snoepjes, noten
). 2.
Je geeft er 3 weg. 3.
Hoeveel hou je over? 4.
Samenvatting in rekentaal:
4 min 3 = 1 (4 min 3 is 1). 1 = 4 - . Hoe
zet je deze bewerking om in taal? 1.
Je hebt 1 euro (of potlood, snoepje, noot
). 2.
Maar je had er 4. 3.
Hoeveel heb je weggegeven (verloren, opgegeten
)? 4.
Samenvatting in rekentaal:
1 = 4 - 3
(1 is 4 min 3). 4 . = 1 Hoe
zet je deze bewerking om in taal? 1.
Je had 4 euro (of potloden, snoepjes, noten
). 2.
Nu heb je nog maar 1. 3.
Hoeveel heb je weggegeven (verloren, opgegeten
)? 4.
Samenvatting in rekentaal: 4 - 3
= 1 (4 min 3 is 1). . 3 = 1 of 1 = . - 3 Hoe
zet je deze bewerking om in taal? 1.
Je hebt 1 euro (of potlood, snoepje, noot
). 2.
Je hebt er 3 weggegeven (verloren, opgegeten
) 3.
Hoeveel had je er? 4 4.
Samenvatting in rekentaal: 4 3 = 1 (4 min 3 is 1). Te onthouden: Het
getal vσσr het minteken geeft altijd aan hoeveel je had. Het
getal nα het minteken geeft altijd aan hoeveel je weggegeven (verloren,
opgegeten
) hebt. Het
gelijkheidsteken kan zowel links als rechts van de opgave staan. Als je de getallen vσσr en nα het minteken een
typische kleur geeft zoals in de voorbeelden hierboven, dan is dit voor de
kinderen nσg duidelijker. Het rode getal is het getal dat aangeeft hoeveel je
hebt of had, het blauwe getal geeft aan hoeveel er weggegeven of verloren of
verdwenen is. Elke mondelinge oefening sluit je af met de
samenvatting in rekentaal. Na verloop van tijd laat je de kleuren weg. ------------------------------------ Vanaf de eerste klas kun je aftrekkingen geven met
drie of meer termen zoals: 7 2 3 = In de mondelinge oefeningen waarbij de kinderen
materialen gebruiken (potloden, steentjes, noten
) oefen je deze regelmatig.
Als dit vlot gaat, geef je ook schriftelijke oefeningen. Kunnen de kinderen
deze oefeningen zelfstandig maken, dan kun je een stap verder gaan door te
laten zien dat je de tweede term bij de derde term kunt optellen en die
uitkomst aftrekken van de eerste term. Dit doe je vooral bij het oefenen aan
de hand van materialen. Bijvoorbeeld: De
kinderen hebben 7 potloden in de linkerhand. Ze
nemen er 2 weg met de rechterhand en daarna nog eens 1. In
hun rechterhand hebben ze dan 3 potloden; in de linkerhand hebben ze nog 4
potloden. Ze
hebben dus eerst dit gedaan: 7 2 = 5 en daarna 5 1 = 4. Maar
daarna stellen ze vast dat ze 3 potloden hebben weggehaald; die hebben ze nu
in de rechterhand. Ze hebben dus eigenlijk dit gedaan: 7
3 = 4 of anders gezegd: ze hebben wat ze weggenomen hebben bijeengeteld en
dan afgetrokken van 7, dus: 7 - (2 + 1) = 4 Waarom laat je hen dit doen? Omdat ze later (in de derde klas en volgende) bij
het cijferend aftrekken dit nodig hebben. Als je bij het cijferen moet
omruilen krijg je drie getallen onder elkaar. Tel je de onderste twee bij
elkaar op, dan kun je sneller rekenen. De bewerking rechts (+1 in de
tientallen) in het voorbeeld hieronder levert hetzelfde resultaat op als de
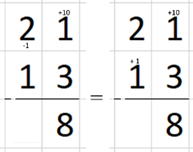
bewerking links (-1 in de tientallen). 1 optellen bij de aftrekker is
hetzelfde als 1 aftrekken van het aftrektal. Een voorbeeld:
De kinderen leren al doende dat 7 2 1 = 4
hetzelfde is als 7 (2 + 1) = 4. Links in het voorbeeld hieronder staat er dus: (7-2) 1 = 4
ofte 5 1 = 4; rechts staat er 7 3 = 4.
------------------------------------ Hiervoor is het nodig dat de getallenrij tot 100
door en door gekend is, wat een opdracht is voor de tweedeklassers. Dit kun
je op verschillende manieren oefenen, maar een van de meest vruchtbare is om
mondelinge oefeningen op de getallenrij te geven met optellen en aftrekken.
De kinderen wijzen hierbij een opgegeven begingetal aan. Daarna moeten ze in
snel tempo, zonder nadenken de getallen aanwijzen die het resultaat zijn van
een opgegeven optelling of aftrekking. Bijvoorbeeld: L
(leerkracht): geeft het getal 7 op. Het kind wijst op de getallenrij het
getal 7 aan. L:
plus 2. Het kind wijst onmiddellijk het getal 9 aan. Is
het fout, dan geeft L zelf het correcte getal en wijst het kind dit getal
aan. Dit gebeurt heel snel, zonder onderbreking en zonder te zeggen dat het
kind een fout heeft gemaakt. Tempo is hier zιιr belangrijk. Als het te traag
gaat, begint het kind te tellen, na te denken en zelfs te twijfelen. Je moet
in elk geval vermijden dat het kind telt.
L:
plus 4. Het kind wijst het getal 13 aan. L:
min 3. Het kind wijst het getal 10 aan. L:
plus 5. Het kind wijst het getal 15 aan. L:
min 6. Het kind wijst het getal 9 aan. Dit
is voldoende per kind. Daarna komt een ander kind aan de beurt. Ik deed
dit zo: Drie
kinderen kregen een stok of een liniaal of iets anders en stonden bij het
bord klaar. Boven op de rand van het bord stond de getallenrij. In de eerste
klas minstens tot 20, maar die rij breidde ik in de loop van het jaar uit,
zodat kinderen die goed konden rekenen ook oefeningen konden maken die
voorbij 20 gingen. Als ιιn kind de oefening gemaakt had, kwam het volgende
kind aan de beurt. Het kind dat klaar was gaf intussen zijn stok/liniaal door
aan een ander kind naar keuze dat dan ging aanschuiven bij het bord. Niet de
hele klas kwam aan de beurt; elke dag een zestal kinderen was meer dan
voldoende, omdat het anders te lang duurde en de kinderen die niet aan de
beurt kwamen zich verveelden. Heb je een opdracht gegeven als 8 + 4 = 12. Dan geef
je onmiddellijk daarna de opdracht: 18 + 4 = 22, en kun je ook de opdracht 38
+ 4 = 42 geven, enzovoort. Of: 13 4 = 9; 33 4 = 29; 73 4 = 69
enzovoort. Dit soort oefeningen geef je veel, zowel mondeling als
schriftelijk. In de voorbeelden hier zie je dat de sommen over het tiental
gaan, zonder de kinderen de opteller (4) of de aftrekker (4) te laten
splitsen. Dat splitsen hoeft ook niet, omdat men, zolang het om hoofdrekenen
gaat, geen extra aandacht hoeft te besteden aan de brug over het tiental. Die
aandacht komt pas als het om cijferen gaat (vanaf de derde klas) en zelfs dan
is dat niet echt noodzakelijk om goed te kunnen rekenen. Voorbeeld van een
opgave:
Je zorgt er in elk geval voor dat de kinderen eind eerste
klas αlle optellingen en aftrekkingen tussen 0 en 20 (ook met overschrijding
van het tiental) uit het hoofd kennen, zodat ze zich in de tweede klas daarop
kunnen baseren bij de optellingen en aftrekkingen tot 100. ------------------------------------ EEN ANDERE SCHRIJFWIJZE (eind tweede klas) Bij
het hoofdrekenen ga je in eerste en tweede klas altijd uit van een
horizontale notatie van de oefeningen. Maar eind tweede klas kun je daar
variatie in brengen door de opgaven verticaal te noteren. Je krijgt dan de
schrijfwijze zoals bij het cijferen, maar je werkt nog volgens het
hoofdrekenen. Hiermee kun je, vooruitlopend op het cijferen, al oefenen op
het recht onder elkaar schrijven van de getallen, zonder daarbij aandacht te
vragen voor eenheden, tientallen, honderdtallen enz. Als je rekenschriften
gebruikt met ruitjes (vakjes) is dat heel eenvoudig te realiseren. Een
oefening als 12 - 4 = . kun je zo noteren:
Slagen
sommige kinderen er niet in om de cijfers mooi onder elkaar te zetten, dan is
dat geen probleem. Stilaan leren ze het en als dan later het decimaal stelsel
geoefend wordt, hebben ze geen probleem meer met het onder elkaar zetten van
de cijfers en kan de aandacht ten volle naar het cijferen gaan. Deze
verticale schrijfwijze helpt ook om al hoofdrekenend
aftrekkingen te maken. Op deze manier leren de kinderen de aftrekkingen van
rechts naar links maken in voorbereiding op wat ze daarna bij het cijferen
zullen doen. Bijvoorbeeld:
83 14 = . Dit
gebeurt meestal door eerst de tientallen van elkaar af te trekken en dan de
eenheden: Eerst
83 10 = 73, daarna 73 4 = 69. Maar
het kan ook door eerst de eenheden van het bovenste getal af te trekken en
daarna de tientallen: Eerst
83 4 = 79, daarna79 10 = 69.
Deze
laatste werkwijze vormt een geschikte overgang naar het cijferen. ------------------------------------ Nadat
bij aanvang van de derde klas het decimaal stelsel is verkend en de kinderen
er voldoende mee geoefend hebben en duidelijk weten dat in een getal de
plaats van een cijfer de waarde van het cijfer bepaalt, kun je beginnen met
cijferend rekenen. De kinderen weten dat 1 tiental gelijk is aan 10 eenheden,
dat 1 honderdtal gelijk is aan 10 tientallen enzovoort. De volgorde van de bewerkingen: 1: Je begint met cijferend optellen, 2: daarna cijferend aftrekken, 3: vervolgens cijferend vermenigvuldigen
(trapvermenigvuldiging) 4: en ten slotte cijferend delen (staartdeling). Het
cijferend aftrekken gebeurt eerst weer met oefeningen die de kinderen met
hoofdreken kunnen oplossen gevolgd door dezelfde opgaven cijferend
uitgewerkt. Omdat ook hier het rekentempo voldoende hoog moet zijn, maak je
de opgaven niet te ingewikkeld en ga je zeker niet boven 100, en met de
eerste oefeningen zelfs niet boven 20. Je zorgt er ook voor dat alle cijfers
van het aftrektal (het bovenste getal) groter zijn dan of gelijk zijn aan de
cijfers van de aftrekker. Bijvoorbeeld:
Eerst
zoeken de kinderen de uitkomst uit het hoofd (18 5 = 13), onmiddellijk
daarna al cijferend (8 5 = 3 en 1 0 = 1). De eerste opgave in
het voorbeeld hierboven: Hoofdrekenen: 18 5 = 13 Cijferen: 8
5 = 3 en 1 - 0 is 1 (als
er gιιn cijfer staat, dan is dat 0). De
tweede opgave: Hoofdrekenen: 14 2 = 12 Cijferen 4
2 = 2 en 1 0
= 1 De derde opgave: Hoofdrekenen: 16 15 = 1 Cijferen: 6 5 = 1 en 1 1 = 0 (een
0 vooraan in een getal schrijf je niet). De vierde oefening
kunnen de kinderen voorlopig alleen met hoofdrekenen oplossen. Cijferend gaat dit nog
niet, maar dat zullen ze later leren. Hoofdrekenen: 11 4 = 7 Cijferen: 1 4 kan niet, want 1 is minder dan 4. Je kunt geen 4 noten opeten als je er maar 1 hebt. Uitbreiding
tot 100.
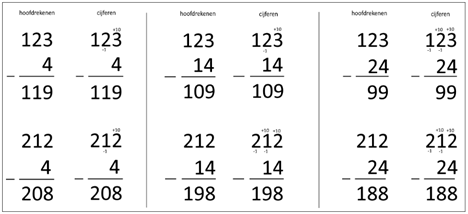
De eerste opgave: Hoofdrekenen: 93 1 = 92
en 92 20 = 72 Cijferen: 3
1 = 2 en 9 2 = 7. De uitkomst (het verschil) is 72.
De tweede opgave: Hoofdrekenen: 74 2 = 72 en
72 30 = 42 Cijferen: 4
2 = 2 en 7 3 = 4. De uitkomst (het verschil) is 42. De derde opgave: Hoofdrekenen: 48 3 = 45
en 45 20 = 25 Cijferen: 8
3 = 5 en 4 2 = 2. De uitkomst (het verschil) is 25. De vierde opgave: Hoofdrekenen: 52 2 = 50
en 50 10 = 40 Cijferen: 2
2 = 0 en 5 1 = 4. De uitkomst (het verschil) is 40. Uitbreiding
tot 1000 in de derde klas. Als
de kinderen intensief geoefend hebben met het decimaal stelsel is het niet
langer nodig om boven elke oefening het decimaal stelsel aan te geven met D
voor de duizendtallen, H voor de honderdtallen, T voor de tientallen en E
voor de eenheden. Wel is het nuttig om regelmatig aan de kinderen (klassikaal
of individueel) te vragen wat de cijfers in de verschillende kolommen
betekenen. Over het algemeen blijft men veel te lang vasthouden aan de
visuele ondersteuning met icoontjes, afkortingen enz., waardoor men de
kinderen verhindert om beroep te doen op hun geheugen en hun verworven
kennis. Omdat
omruilen (lenen, omwisselen) voorlopig nog niet aan de orde is, zijn alle cijfers
van het aftrektal groter dan of gelijk aan de cijfers van de aftrekker.
Bijvoorbeeld:
Ook
bij deze oefeningen kun je zowel met hoofdrekenen als met cijferen werken. Met
hoofdrekenen laat je de tussenuitkomsten onder de opgave noteren. Je trekt
van het aftrektal eerst de eenheden af, dan de tientallen en ten slotte de
honderdtallen. Het onderste getal is de uitkomst. Je krijgt dit als
resultaat:
Met
deze werkwijze ervaren de kinderen duidelijk dat het tweede cijfer in de
aftrekker gelijk is aan 40 (eerste opgave) en 10 (tweede opgave) en dat het
voorste cijfer gelijk is aan respectievelijk 300, 600, 500 en 100. De eerste opgave in
het voorbeeld hierboven: Hoofdrekenen: 567 5 = 562 →
562 40 = 522 → 522 300 = 22. Cijferen: 7 5
= 2 en 6 4 = 2 en 5 3 =
2. De tweede opgave: Hoofdrekenen: 678 2 = 676 →
676 10 = 666 → 666 600 = 66. Cijferen: 8 2
= 6 en 7 1 = 6 en 6 6 = 0
(hoef
je niet te schrijven). De derde opgave: Hoofdrekenen: 804 4 = 800 →
800 0 = 800 → 800 500 = 300 (0
aftrekken hoef je niet te doen en mag je overslaan). Cijferen: 4 4
= 0 en 0 0 = 0 en 8 5 =
4. De vierde opgave: Hoofdrekenen: 219 8 = 211 →
211 100 = 111. Cijferen: 9 8
= 1 en 1 0 = 1 en 2 1 =
1. Je
hoeft niet altijd met het aftrekken van de eenheden te beginnen, al is dat
wel de beste voorbereiding op het cijferen; je kunt ook met de honderdtallen
beginnen en dus van links naar rechts werken. Ook bij deze manier van werken
kun je de tussenuitkomsten noteren.
De bewerking gebeurt
als volgt: eerst 567
300 = 267
dan 267
40 = 227
ten slotte 227 5 = 222
------------------------------------ AFTREKKEN MET OMRUILEN (omwisselen, lenen) Als het
cijfer van de eenheden (E) in de aftrekker groter is dan het cijfer erboven
in het aftrektal, kun je de aftrekking niet maken tenzij je in de kolom van
de tientallen (T) ιιn tiental afneemt van het aftrektal en dat bijvoegt bij
de eenheden van het aftrektal. Zo
gaat het ook als een cijfer van het aftrektal in een van de andere kolommen
kleiner is dan het cijfer eronder: je haalt ιιn weg uit de kolom links ervan
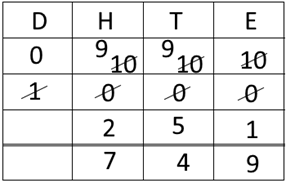
en voegt dit als tien toe aan het cijfer van het aftrektal. Meestal
gebruikt men een methode die er zo uitziet:
Deze
werkwijze heeft enkele nadelen: Het originele aftrektal verdwijnt achter
doorgestreepte cijfers. Ze is niet mooi met die doorgestreepte cijfers en
al zeker niet als je twee cijfers boven elkaar doorstreept. Ze is visueel niet sterk, want je ziet niet dat je
1 hebt weggehaald tenzij je het doorstreepte cijfer vergelijkt met het cijfer
erboven. Ze is complex, zeker als je twee of drie kolommen
ver moet gaan om een cijfer om te wisselen. De
methode die ik gebruik omzeilt die nadelen en maakt het rekenwerk een stuk
mooier en vooral eenvoudiger omdat je kolom per kolom kunt uitrekenen zonder
eerst naar de volgende kolommen te moeten gaan om een getal om te wisselen
als er nullen in het aftrektal staan. Het
voorbeeld hieronder laat de evolutie van de werkwijze zien. Eerst werken de
kinderen zoals in het voorbeeld links. Korte tijd later schrijven
ze de oefening op zoals in het 2e voorbeeld. Daarna vervangen ze de
cijfers door stippen. Ten slotte werken ze
zonder de stippen zoals in het voorbeeld rechts.
De
voordelen van deze werkwijze: Het originele aftrektal blijft duidelijk
zichtbaar. Ze heeft geen doorstreepte getallen; ze is dus
mooier. De kinderen leren getallen heel klein schrijven (-1 en +10). Ze is visueel sterk, want wat je gedaan hebt
blijft zichtbaar (-1 en +10). Het is niet nodig om de kolommen te benoemen met D
H T E, want dat is gekende leerstof en de kinderen zouden nu wel moeten
weten welke kolommen eenheden, tientallen enz. voorstellen. Het is altijd
beter de visuele voorstelling zo snel mogelijk achterwege te laten en beroep
te doen op het geheugen. Ze evolueert. De schrijfwijze -1 en +10 wordt
al snel gewijzigd in +1 en +10 en korte tijd later vervangen door stippen.
De stip boven het onderste cijfer heeft de waarde +1, de stip boven het
bovenste cijfer heeft de waarde +10. Nog later worden de stippen achterwege
gelaten en onthouden de kinderen alleen nog het riedeltje: plus 1, plus
10 en voor goede rekenaars is zelfs dat niet meer nodig. Didactiek Je
begint met opgaven met eenheden en tientallen die de kinderen uit het hoofd
kunnen maken, onmiddellijk gevolgd door dezelfde opgave al cijferend te
maken. Je vergelijkt de twee uitkomsten. Bij
het cijferen stel je vast dat bij de eenheden de aftrekking niet mogelijk is
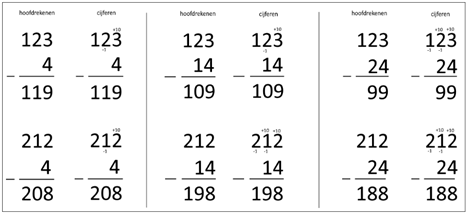
en dat je daarom een tiental omruilt met 10 eenheden. Bijvoorbeeld
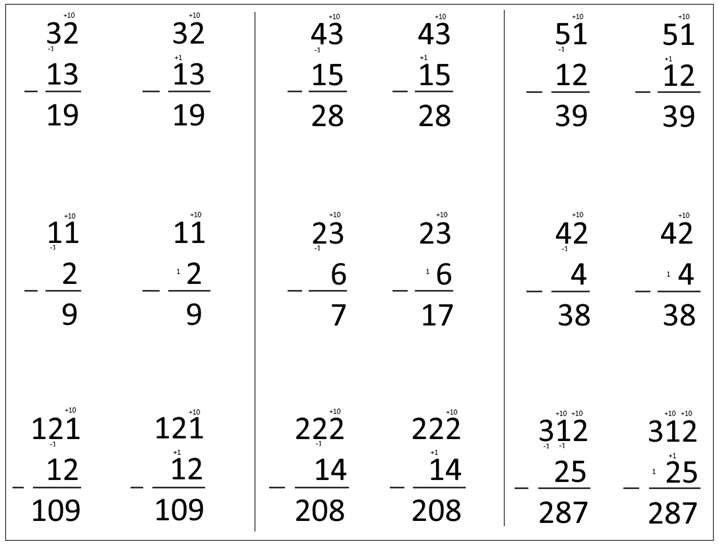
voor de opgave 12 4 in het kader hieronder: 2
4: kan niet, dus ruil ik ιιn tiental om met 10 eenheden. Ik schrijf -1 onder
het tiental en +10 boven de eenheden. 12
4 = 8. 1 1:
nul (hoef je niet te schrijven aangezien ze vooraan in het getal staat). De uitkomst is 8. De
opgave 22 4 gaat cijferend zo: 2 4:
kan niet, dus ruil ik ιιn tiental om met 10 eenheden. Ik schrijf -1 onder het
tiental en +10 boven de eenheden. 12
4 = 8 2
1 = 1 De uitkomst is 18.
Dit kan
ook met opgaven met eenheden, tientallen en honderdtallen, al zal dat bij de
aanvang van de derde klas nog niet vanzelfsprekend zijn aangezien je de
getallenrij nog aan het uitbreiden bent tot 1000, waardoor hoofdrekenen met
getallen boven 100 nog niet zo vlot gaat. Nieuw bij het cijferen is dat je,
als het nodig is, een honderdtal moet omruilen voor 10 tientallen.
Is
het principe van omruilen gekend, dan kun je -1 vervangen door +1. Je
zet twee dezelfde opgaven naast elkaar, links werk je uit met -1 en +10,
rechts werk je uit met +1 en +10.
Kunnen
de kinderen goed overweg met deze werkwijze, dan kun je nog een stap
verdergaan en +1 en +10 vervangen door stippen boven de cijfers. Een stip
boven een cijfer in het aftrektal heeft de waarde +10, een stip boven de
cijfers van de aftrekker heeft de waarde +1. Bijvoorbeeld:
TUSSENDOOR EN TERZIJDE De opgaven in het
kader hierboven hebben speciale uitkomsten. Hier gaan de uitkomsten in
stijgende lijn als je de cijfers ervan optelt: 10
11 12 13 14 15. Ik gaf veel van zulke
opgaven waarbij er in de uitkomsten een verrassing verborgen zat. Op die
manier kon ik extra rekensommen geven (in dit geval optellingen) en leerden
de kinderen om de uitkomsten aandachtiger te bekijken. Ten
slotte kun je de kinderen die goed kunnen rekenen vragen om de stippen weg te
laten. In de vijfde en zesde klas is dat voor veel kinderen geen probleem.
Zonder de stippen (en dus ook zonder -1/+1 en +10) gebruiken ze hun geheugen
beter en gaat het rekenen ook sneller. Gebruik van het werkgeheugen zonder
visuele ondersteuning en een goed tempo aanhouden
bij het rekenen vind ik vιιl belangrijker dan moeilijke opgaven geven.
De kinderen vinden rekenen daardoor uitdagender en ze maken veel meer
oefeningen, waardoor hun kennis vergroot. Omdat
ik haast dagelijks minstens ιιn staartdeling opgaf dikwijls gecombineerd
met optelling en vermenigvuldiging kwamen aftrekkingen met en zonder
omruilen (lenen) veel aan bod. Al ga
je wat getallenkennis betreft maar tot 1000 in de derde klas, toch kun je bij
het cijferen, zodra het voldoende gekend is, met veel grotere getallen
werken. Geleidelijk leren de kinderen deze getallen benoemen. Ze vinden het
trouwens heel leuk om grote getallen correct te kunnen uitspreken.
De opgave hierboven
heeft ook een extra laag: als je de uitkomst omdraait en erbij optelt, krijg je
een uitkomst die iets verrassends heeft (allemaal cijfers 5, eerste + laatste
cijfer is ook 5):
------------------------------------ Moeten
de kinderen de uitkomst van een oefening met cijferen kunnen schatten vσσr ze
de opgave uitwerken? Dit kan, maar hoeft zeker niet bij elke opgave te
gebeuren. Nu en dan als een opfrissing is het heel goed, maar het is voor hen
ook heel interessant om gewoon een reeks opgaven al cijferend uit te werken
zonder geconfronteerd te worden met het schatten van de uitkomst. Het is
daarbij ook zinvol om, als de uitkomst met cijferen gevonden is, opgave ιn
uitkomst te laten voorlezen en van commentaar te voorzien door te verwijzen
naar de praktijk: waar kom je zulke getallen tegen? ------------------------------------ Is de
gevonden uitkomst correct? Je
kunt minstens drie manieren gebruiken om de uitkomst te controleren: 1. De oefening omdraaien: van de aftrekking een
optelling maken. 2. De negenproef. 3. Het rekentoestel. 1.
De optelling. Je
telt de uitkomst op bij de aftrekker. Het resultaat is gelijk aan het
aftrektal.
0 + 2 + 1 = 3 in de kolom van de tientallen en bij de
honderdtallen zie je 1 = 1. 2. De negenproef.
De cijfersom van de aftrekker = 11. De
cijfersom daarvan = 2. De cijfersom van de uitkomst = 11. De
cijfersom daarvan is 2. Het verschil
tussen de cijfersommen van aftrektal en aftrekker is 2. 2 is ook de
cijfersom van de uitkomst. Resultaat: de aftrekking is correct. (Is de
cijfersom van het aftrektal kleiner dan de cijfersom van de aftrekker, dan
tel je bij de cijfersom van het aftrektal 9 bij.) Naast optelling
en negenproef kun je ook het rekentoestel gebruiken. In de 5e en de 6e klas
gebeurt dit in de lessen rekenen en ICT. Het kan ook een van de eerste
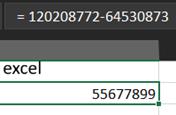
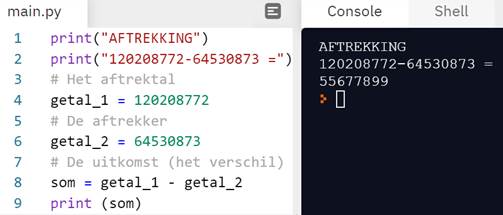
toepassingen zijn bij het leren programmeren. In het voorbeeld hieronder zie
je links het rekentoestel van Windows op pc, rechts de oefening in Excel,
daaronder de oefening op de command line in Python
en daaronder als een programma in de editor van Python.
|