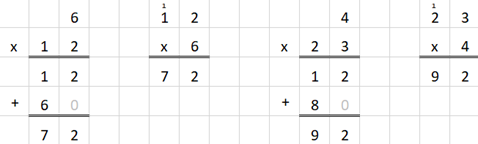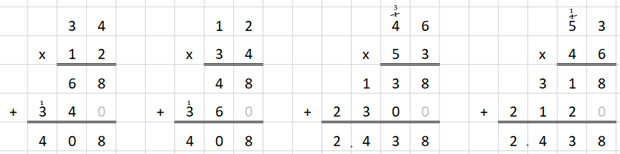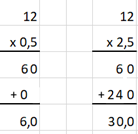|
CIJFEREN: DE
TRAPVERMENIGVULDIGING Luc
Cielen Ik noem dit een trapvermenigvuldiging omdat deze
bewerking een trap vormt als de vermenigvuldiger een getal is met 2 of meer
cijfers.
In een opbouw die 12 dagen duurt, wordt er elke
dag een kleine stap gezet. Op elke stap maken de kinderen een twintigtal
oefeningen. Daarnaast is er dan voldoende tijd om andere zaken uit rekenen en
taal en andere vakken te herhalen. Elke dag voorzie je dan ook diverse
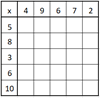
herhalingsopdrachten over eerder behandelde leerstof, zoals: Een maaltafelvierkant (zie https://www.cielen.eu/rekenvierkanten.htm):
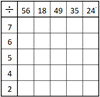
Een
deeltafelvierkant (zie https://www.cielen.eu/rekenvierkanten.htm):
Een
rekendictee (zie https://www.cielen.eu/rekendictees.htm): We hebben thuis 12 bessenstruiken, 8
vlierstruiken, 8 meidoorns en 6 rozenstruiken geplant. Door de droogte zijn 7
planten doodgegaan. Hoeveel planten zijn in leven gebleven? Enkele
opgaven over cijferend optellen:
Enkele
opgaven over cijferend aftrekken:
Enkele
opgaven over metend rekenen (als dit al aan bod gekomen is): Mijn broer en ik fietsen elke dag 4 km van
thuis naar school. Hoeveel km leggen we samen af op één schoolweek van thuis
naar school en terug? Teken op een analoge klok: 5 over 8 * 10
voor 7 * kwart na 4 Trapvermenigvuldiging: enkele oefeningen
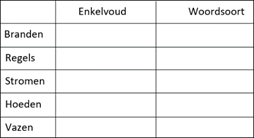
over één of meer van de vorige stappen. Enkele taaloefeningen (spelling,
woordsoorten, raadsel, creatief schrijven …).
------------------------------------ Waarom
deze bewerking aanleren in kleine stappen? Omdat de kinderen dan tijd hebben om elke
nieuwe stap te verwerven vóór ze de volgende stap zetten en zo geleidelijk
tot inzicht in de bewerking kunnen komen. Een omslachtige uitleg is niet
nodig, het kan kort waardoor de kinderen snel aan het werk kunnen. Door deze
werkwijze kun je steeds voortbouwen op wat al gekend is. ------------------------------------ DAG 1 Hoofdrekenen met verticale notatie De opgaven zet je in kolommen met hoofding T
voor de tientallen en E voor de eenheden, al is dit niet per nodig aangezien
het tientallig stelsel al voldoende gekend zal zijn als de vermenigvuldiging aan
de beurt komt. Wel is het zinvol om de getallen telkens te lezen en nu en dan
ook te vragen welk getal elk cijfer voorstelt. Het onderscheid tussen cijfer
en getal moet dan ook duidelijk zijn. Tegelijk met het inoefenen van de
trapvermenigvuldiging herhalen de kinderen voortdurend de maaltafels. Het
gelijkheidsteken (de dubbele lijn) staat onder de opgave.
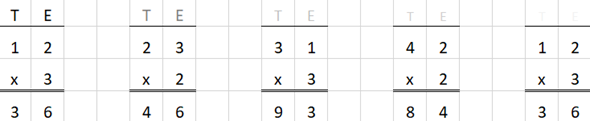
------------------------------------ DAG 2 Een getal van 2 cijfers vermenigvuldigen met
een getal van 1 cijfer zonder overschrijding van het tiental. Je kunt de oplossing eerst laten
schatten of uit het hoofd laten maken. Op dag 1 heb je bij het
hoofdrekenen tussen de opgaven al eens een getal met 2 cijfers in het
vermenigvuldigtal gezet. Deze opgave kun je nu als voorbeeld nemen om te
laten zien dat je dezelfde uitkomst ook cijferend kunt vinden. In het
voorbeeld hieronder laat ik de titels T en E geleidelijk verdwijnen.
Na het cijferen laat je de uitkomst lezen. ------------------------------------ DAG 3 Een getal van 3 cijfers vermenigvuldigen met
een getal van 1 cijfer zonder overschrijden van het tiental. Eerst schatten, dan proberen uit
het hoofd te rekenen, dan cijferen en ten slotte het getal van de uitkomst
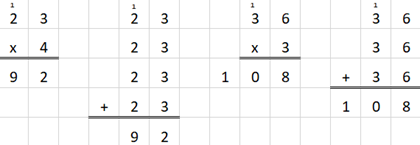
lezen. Bijvoorbeeld: 1. Schatten: de
eerste opgave: het getal bovenaan is meer dan 100, minder dan 200. Maal 3
geeft dat een uitkomst tussen 300 en 400. 2.
Hoofdrekenen: 100 x 3 = 300 * 20 x 3 = 60 * 3 x 3 = 9. Samen is dat: 300 + 60
+ 3 = 369. 3. Cijferen:
eerst de eenheden, dan de tientallen, dan de honderdtallen. 4. De
uitkomsten lezen: driehonderdnegenenzestig.
Belangrijk bij deze stap is het lezen van de
getallen (derde klas = getallenkennis tot 1000) en het bepalen van de waarde van elk
cijfer. Welk getal stelt
het cijfer 1 voor in de eerste opgave? 100. Welk getal
stelt het cijfer 2 voor in de eerste opgave? 20. Welk getal
stelt het cijfer 3 voor in de eerste opgave? 3. Welk getal
stelt het cijfer 3 voor in de uitkomst van de eerste opgave? 300. Enz. ------------------------------------ DAG 4 Getallen van meer dan 3 cijfers
vermenigvuldigen met een getal van 1 cijfer zonder overschrijden van het
tiental. Getallenkennis in de derde klas gaat tot
1000, maar dat wil niet zeggen dat de kinderen grotere getallen niet mogen
lezen. Dat ze zich er niet veel bij kunnen voorstellen is hier niet zo
belangrijk, het gaat nu vooral over het cijferen, maar het is wel zinvol om
hun af en toe enig idee te geven van de grootteorde van de getallen. Met het
getal 1000 kom je in de buurt van wat een persoon in België nodig heeft om
maandelijks rond te komen. Met 10.000 zit je in de categorie van wat een auto
kost. Met 100.000 kom je bij bedragen die omgaan in aankoop van huizen en
appartementen. Met 1.000.000 en miljoenen goochelen de politici, wat kinderen
via nieuwsmedia al wel eens opvangen. Lezen van getallen moet je ook oefenen,
want in het Nederlands is dat minder vanzelfsprekend dan in het Engels of het
Frans. In die talen leest men getallen consequent van links naar rechts. In
het Nederlands is dat anders: daar lezen we van links naar rechts naar links
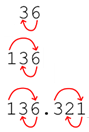
naar rechts: steeds afwisselend. Bijvoorbeeld: 123 lees je eerst de
honderdtallen, dan de eenheden en ten slotte de tientallen. Zo gaat het
steeds voort in groepjes van drie cijfers bij getallen groter dan 1000.
De kinderen weten intussen dat ze bij het
cijferen rechts (= eenheden) beginnen en zo elk cijfer van het
vermenigvuldigtal opschuivend naar links moeten vermenigvuldigen met de
vermenigvuldiger. Bijvoorbeeld:
Duidelijkheidshalve kun je een punt (stip)
zetten of een spatie invoegen tussen de duizendtallen en de honderdtallen. Het overschrijden van het tiental zoals bij
4 x 3 = 12 levert geen probleem op als dat gebeurt bij het meest linkse
cijfer van het vermenigvuldigtal. Het is goed enkele opgaven te voorzien
waarbij dit gebeurt als voorbereiding op de volgende stap. ------------------------------------ DAG 5 Een getal van 2 cijfers vermenigvuldigen met
een getal van 1 cijfer mét overschrijding van het tiental vertrekkend van het hoofdrekenen, maar met
een andere schrijfwijze dan in de eerste en de tweede klas. Bijvoorbeeld:
Het te onthouden cijfer laat je bovenaan in
de kolom links zetten. (Er bestaan andere werkwijzen daarvoor: het
te onthouden cijfer wordt bijvoorbeeld onderaan geschreven of rechts van de
oefening. Ik geef er de voorkeur aan om onmiddellijk de schrijfwijze te
gebruiken die later toch gebruikt zal worden. Je hoeft er slechts op te
wijzen dat de 12 zo geschreven wordt dat de 1 bovenaan in de kolom links
staat en 2 onderaan in de kolom rechts. Deze schrijfwijze is louter en alleen
conventie en daarom niet in die mate belangrijk dat er ook nog eens een
andere schrijfwijze aan vooraf moet gaan. In de loop van de 5e en zeker in de
6e klas hoeft het te onthouden cijfer niet meer genoteerd te worden. De
kinderen moeten leren dit cijfer te onthouden zonder te noteren.) ------------------------------------ DAG 6 Getallen met 2 cijfers vermenigvuldigen met
een getal van 1 cijfer, maar nu met hogere getallen dan de gekende tafels uit
het hoofdrekenen. Controleer de
uitkomst door een optelling te maken. Ook nu kun je voorafgaand aan het
cijferen de oplossing laten schatten. Bijvoorbeeld:
Controleren met een optelling is hierbij
absoluut nodig om inzicht te krijgen in wat er gebeurt bij de
vermenigvuldiging. Als je een twintigtal opgaven geeft, hoeven niet al die
oefeningen gecontroleerd te worden. Je kunt per kind een keuze maken van
welke opgaven het wél en welke het niet met een optelling moet controleren. ------------------------------------ DAG 7 Getallen van 3 cijfers vermenigvuldigen met
een getal van1 cijfer en controleren met een optelling. Eerst weer schatten en na het
vermenigvuldigen controleren met een optelling. De uitkomst lezen.
Bijvoorbeeld:
------------------------------------ DAG 8 Getallen van meer dan 3 cijfers
vermenigvuldigen met een getal van 1 cijfer en controle van enkele opgaven
met een optelling. De getallen lezen. Bijvoorbeeld:
------------------------------------ DAG 9 Een getal van 1 cijfer vermenigvuldigen met
een getal van 2 cijfers. Weer
vertrekken vanuit het hoofdrekenen. Het cijfer 0 onder de 6 in de kolom van
de eenheden in het eerste voorbeeld kun je in een andere kleur of héél zacht
laten schrijven. Vanaf dag 12 kun je de kinderen die er geen behoefte meer
aan hebben, vragen om de 0 weg te laten. Controle kan gebeuren door de opgave
om te draaien: het vermenigvuldigtal wordt vermenigvuldiger en vice versa:
De tussenoplossingen en de einduitkomst
laten lezen:
2 maal 6 is 12
3 maal 4 is 12 10 maal 6 is 60 20 maal 4 is 80 12 maal 6 is 72 23 maal 4 is 92 ------------------------------------ DAG 10 Een getal van 2 cijfers vermenigvuldigen met
een getal van 2 cijfers. Controle
door de opgave om te keren. Als er tweemaal een cijfer moet onthouden worden,
mogen de kinderen het cijfer dat niet meer gebruikt wordt doorstrepen, maar
dit is geen verplichting. De getallen laten lezen. Ook de tussenoplossingen en de uitkomst
laten lezen: 2 maal 34 is 68 3 maal 46 is 138 10
maal 34 is 340 50 maal 46 is
2.300 12
maal 34 is 408 53 maal 46 is
2.438 ------------------------------------ DAG 11 Trapvermenigvuldigingen met meer dan 2
cijfers in de vermenigvuldiger.
Regelmatig laat je van een oefening de
tussenuitkomsten en de einduitkomst lezen. ------------------------------------ DAG 12 en
volgende: Je laat elke dag minstens 1 trapvermenigvuldiging
maken. Af en toe zet je meer cijfers in het vermenigvuldigtal en nu en dan
zet je meer cijfers in de vermenigvuldiger. Hoe meer cijfers in de
vermenigvuldiger hoe langer de trap wordt. Stilaan mogen de cijfers 0 die in de
voorbeelden hierboven in het grijs staan, verdwijnen. Als je deze nullen
weglaat, is de trap duidelijker en kunnen de kinderen ook beter zien in welke
kolom ze werken. ------------------------------------ In
de 4e
klas volgt de vermenigvuldiging met komma. Stap 1: een klein getal met 1 cijfer na de
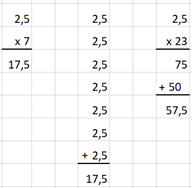
komma in het vermenigvuldigtal. Controle via optelling. Voorbeeld:
2,5 x 7 = (met controle) en 2,5 x 23 = (zonder controle)
Stap 2: een klein getal met 2 cijfers na de
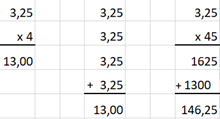
komma in het vermenigvuldigtal. Controle via optelling. Voorbeeld:
3,25 x 4 = (met controle) en 3,25 x 45 =
(zonder controle)
Stap 3: een getal met 3 cijfers na de komma
in het vermenigvuldigtal. Controle via optelling. Voorbeeld:
5,125 x 3
= (met controle) en 5,125 x 27 = (zonder controle)
Stap 4: grotere getallen met 1, 2 of 3
cijfers na de komma. Controle via optelling van enkele opgaven waarvan de
vermenigvuldiger niet te groot is. Stap 5: een klein getal zonder komma in het
vermenigvuldigtal, klein getal met 1 cijfer na de komma in de
vermenigvuldiger. Geen controle via optelling. Voorbeeld:
12 x 0,5 = en
12
x 2,5 = Vragen stellen als: Wat betekent dit:
vermenigvuldigen met 0,5? Of met een half? Dit betekent: het getal
halveren. Vermenigvuldigen met 2,5 =
het getal twee keer nemen en nog een half erbij. Dus in het voorbeeld 12 x
2,5 is dat 12 x 2 plus 6.
Stap 6: een klein getal zonder komma in het
vermenigvuldigtal, een klein getal met 2 cijfers na de komma in de
vermenigvuldiger. Voorbeeld:
12 x 0,25
= en 12 x 3,25 = Zelfde
bespreking als in stap 5.
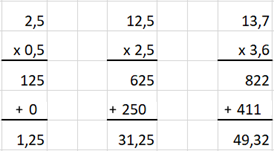
Stap 7: een klein getal met 1 cijfer na de
komma in het vermenigvuldigtal en een klein getal met 1 cijfer na de komma in
de vermenigvuldiger. Voorbeeld: 2,5 x 0,5 = en 12,5 x 2,5 = en 13,7 x 3,6 = Bespreking na het maken van enkele
oefeningen: Hoeveel cijfers komen er in de uitkomst na de komma? Vergelijk
dat met het aantal cijfers na de komma in de opgave.
Stap 8: Vermenigvuldigtal: een klein getal
met 2 cijfers na de komma. Vermenigvuldiger:
een klein getal met 1 cijfer na de komma. Voorbeeld:
12,7 x
3,24 = Zelfde
bespreking als in stap 7.
Stap 9: Zoals stap 8 met grotere getallen en
met 1, 2 of 3 cijfers na de komma.
------------------------------------ Als deze opbouw voltooid is zal de controle
regelmatig gebeuren door het maken van een staartdeling. Elke dag mag er
minstens 1 opgave zo gecontroleerd worden. De negenproef wordt ook in de vierde klas
aangeleerd. Die geeft echter niet steeds uitsluitsel of een bewerking al dan
niet correct is uitgevoerd. Daarom wordt de negenproef niet te nadrukkelijk
geoefend. Beter is om een trapvermenigvuldiging met een staartdeling te
controleren en een staartdeling kan met een trapvermenigvuldiging
gecontroleerd worden. Geef
je dagelijks 1 staartdeling op die je laat controleren met een
trapvermenigvuldiging, dan heb je de vier hoofdbewerkingen in één opgave. ------------------------------------ LINKEN Cijferen:
trapvermenigvuldiging |